
Crowne Plaza Hotel, Seattle, USA
In order to support multiple real-time applications on a single platform, the operating system must provide Quality of Service (QoS) guarantees so that the system resources can be provisioned among applications to achieve desired levels of predictable performance. The traditional QoS parameters include fairness, delay, and throughput. In this paper we introduce a new QoS criterion called cumulative service. The cumulative service criterion relates the total service obtained by a process under a scheduling policy to the ideal service that the process would have accumulated by executing on each resource at a reserved rate. We say that a scheuling policy provides a cumulative service guarantee if the performance of the real system differs from the ideal system by at most a constant amount. A cumulative service guarantee is vital for applications (e.g., a continous media file service) that require multiple resources and demand predictable aggregated throughput over all these resources. Existing scheduling algorithms that guarantee traditional QoS paramaters do not provide cumulative service guarantees. We present a new scheduling algorithm called Move-To-Rear List Scheduling which provides a cumulative service guarantee as well as the traditional guarantees such as fairness (proportional sharing) and bounded delay. The complexity of MTR-LS is O(ln(n)) where n is the number of processes.
Quality of service, cumulative service, resource reservation, scheduling algorithm
New multimedia applications, which require support for real-time processing, are pacing the demand for operating system support for Quality of Service (QoS) guarantees. The desire to support multiple real-time applications on a single platform requires that the operating system have the ability to provision the system resources among applications in a manner that achieves the desired levels of predictable performance. Moreover, computer networks are starting to provide QoS guarantees with respect to packet delay and connection bandwidth. These QoS guarantees are of little use if they cannot be extended to the endpoint applications via operating system support for related QoS parameters. Current general-purpose multiprogrammed operating systems do not provide QoS guarantees since the performance of a single application is, in part, determined by the overall load on system. As a result many users prefer to use stand-alone systems with limited dependency on shared servers to achieve some semblance of QoS by indirectly controlling the system workload. Real-time operating systems are capable of delivering performance guarantees such as delay bounds, but require that applications be modified to take advantage of the real-time features. Our goal is to provide QoS guarantees in the context of a general-purpose multiprogrammed OS, without modification to the applications, by giving the user the option to provision system resources among applications in order to achieve the desired performance levels.
In this paper we introduce a new QoS parameter, which we call the Cumulative Service. Guaranteeing cumulative service is vital for applications that require multiple resources and demand a predictable aggregate throughput over these resources. We present a new scheduling algorithm, called Move-To-Rear List Scheduling (MTR-LS), for allocating operating system resources, such as CPUs, disks, and network interfaces, among competing processes. We show that MTR-LS provides strict guarantees regarding the cumulative service obtained by a process. MTR-LS also provides guarantees for more traditional QoS parameters such as fairness and delay.
Our results are applicable to a general model of processes. However, for ease of exposition we define a process to be a sequence of phases (Section 3) where each phase consists of a requirement from a particular system server. It is assumed that neither the phase requirements nor the exact sequence of phases are known ahead of time. Our model allows for new processes to dynamically enter the system and for processes to depart the system. Processes specify their QoS requirements by providing a ``service fraction'' for each system resource. Admission control consists of ensuring that the service fractions of new processes along with the service fractions of processes already in the system do not exceed certain prescribed limits. Admission control is necessary if we are to provide delay and cumulative service guarantees that are independent of the number of processes in the system.
Another feature of our work is that it deals with system services that have limited preemptability. For example, disk I/O occurs in multiples of a basic block size and once a transfer is begun, the next scheduling event can not occur before the transfer is complete. However, the granularity for CPU scheduling is taken to be arbitrary.
Our cumulative service QoS parameter is new. The cumulative service criterion compares the total service accumulation of a process at a server to an ideal service accumulation based on the service fraction of the process for this server (we will use resources and servers, interchangeably). We say that a scheduling policy guarantees cumulative service if the total service obtained over any time interval does not fall behind the ideal service accumulation, based on the service fraction, by more than a constant amount. In our ideal system we assume that a processes gets its specific service fractions of each of the resources without interference from other processes. This corresponds to a processor sharing model in which the servers are not overbooked, i.e. the sum of the service fractions at each server is not greater than one. Recall that we model processes as a sequence of phases where each phase corresponds to a service requirement from a particular server. In spite of the fact that the delay incurred by a phase of a process at one server is propagated to subsequent phases of the process at the same server and other servers, we will show that the MTR-LS policy provides a cumulative service guarantee over every interval of time.
The QoS parameters supported by many existing scheduling algorithms include proportional sharing of the CPU among competing processes and delay bound guarantees [8, 11, 5, 10]. However, they do not support a cumulative service guarantee since neither fairness nor delay bounds are sufficient to provide a cumulative service guarantee. Informally, guaranteed cumulative service means that the scheduling delays encountered by a process on various resources do not accumulate over the lifetime of the process.
The cumulative service criterion is essential for providing aggregate service for applications that require the sequential use of multiple resources such as CPU and disk. It is especially vital for such applications that act as services. A good example is a continuous media (CM) file service, which shares system resources with other applications or services, that itself is in a position to provide certain QoS guarantees to other applications. A typical implementation of a streaming CM file service assumes that it can sustain a certain amount of disk I/O throughput. However, it also needs CPU for tasks such as initiating disk requests, and managing its buffers, etc.
Example 1:
To make our point, let us consider the following overly simplified CM server:
1) An entire disk drive with an effective bandwidth
of 40 Mbps and half of the CPU cycles are reserved for this service.
2) In between every 1 MB of disk I/O, the CM server requires 1 ms
of real CPU time to dispatch disk requests and manage the buffers.
Since it reserved half of the CPU, it expects that the execution time
for each CPU phase will take at most 2 ms.
Similarly, since it reserved
the entire disk, it expects that each disk phase
(i.e., 1 MB disk I/O) will take 200 ms.
Thus, the CM server expects a disk I/O throughput
of 1MB/202ms= 39 Mbps.
The CPU delay bound provided by
existing algorithms
[11, 5, 10]
depends upon, among other things, the granularity of scheduling quanta.
The granularity cannot be too small for otherwise the context switching overhead would
become excessive.
It would not be unusual to have a CPU delay bound of 75 ms.
That is, the CPU scheduler promises
that each CPU phase
of length t will complete within
t/ 0.5+75 ms.
The t/0.5 results from reserving half of the CPU and the 75 ms is due to
an average delay of 75 ms for other processes to get their
time-slice.
Suppose that each CPU phase of the CM server
waits 75 ms for the other processes contending
for CPU before it executes
for 1 ms on CPU.
A 76 ms delay for 1 ms CPU execution is still
within the delay bound promised by the CPU scheduler.
However, the disk I/O throughput of the CM server will degrade
to 1MB/276ms = 28 Mbps!
This is 30% less than expected.
Under these circumstances, the CM server could not support
26 streaming MPEG-1 sessions, each
requiring a 1.5 Mbps throughput
(26 x 1.5 Mbps = 39 Mbps).

The main contributions of this work are the introduction of the cumulative service criterion as an important QoS parameter for OS scheduling and the MTR-LS policy which provides a cumulative service guarantee and guarantees for other QoS parameters including fairness (proportional sharing) and delay bounds.
The remainder of the paper is organized as follows. QoS parameters and theoretical developments in terms of deterministic performance bounds are well developed in the link scheduling literature. In the next section we review some of the relevant aspects of link scheduling since they are closely related (both in terms of similarities and differences) to their counterparts in operating systems. Following this, we discuss the QoS parameters that play a role in our work. In Section 3 we introduce our system and process models and definitions of QoS parameters. in Section 4, we present a new scheduling policy, called Move-To-Rear List Scheduling, that is fair and provides a cumulative service guarantee. Finally, Section 5 summarizes our work.
The QoS issue has received much attention in the packet scheduling literature [2, 13, 4, 12, 6] where packets are identified with ``flows'' and there is a, conceptual, queue per flow or collection of flows. The correspondence between a sequence of packets and a flow is application-dependent, but we assume that we can identify packets belonging to a particular flow.
The objective for the link scheduler is to determine the order in which packets are scheduled for transmission on the output link so as to achieve various performance measures. We review some of the QoS parameters for output link scheduling and contrast these with QoS support for processes in the operating system context where there are important similarities and differences.
We assume that when a packet arrives at a node a routing table lookup is performed to determine the appropriate output link and a (possibly concurrent) flow identification lookup is done to determine the appropriate queue. Although there is a delay associated with these steps, they tend to be uniform over the packets. We take the arrival of a packet at a queue as an instantaneous event corresponding to the placement of a record, which gives the specifics of the packet data, in the appropriate queue data structure.
There are roughly two kinds of packet sources, open-loop and closed-loop. For an open-loop packet source the times-of-arrival of packets are not affected by the delay experienced by packets that have already arrived. A closed-loop packet source is one for which the times-of-arrival may be affected by the delays experienced by packets that have already arrived. Open-loop sources include unacknowledged transmission of UDP packet streams. Closed loop sources include TCP/IP flows.
The QoS parameters in link scheduling include delay, delay jitter, throughput, and fairness. Packet delay can be measured in a number of ways. The delay can be measured from the time that the packet arrives at its queue until it is transmitted over the link. This measure of delay depends on the behavior of the traffic source and the scheduling policy. Another possibility is to measure the delay of the packet from the time it reaches the head of its queue until it is transmitted over the output link. This measure of delay does not depend on the characteristics of the traffic source. Yet another possibility is to assume that each flow is provided a certain bandwidth reservation and calculate the departure time of each packet based on the assumption that all the packets in the flow are serviced at the reserved bandwidth rate. The delay of a packet is the difference between the packet's actual departure time and its calculated departure time (may be negative). This delay measures the real system's ability to match the performance of an idealized system.
Delay jitter is a measure of the variability of packet delay. The minimization of delay jitter is important in situations where the receiver buffers packets from a flow and plays them out at a constant rate. The more variable the jitter, the larger the buffer needed to regulate the flow for smooth playout.
Throughput is a measure of the rate at which the data from a flow is transmitted over the link. Determination of the throughput of a flow depends on the time scale used to measure the transmission rate. For example, the instantaneous transmission rate of data in a flow has two possible values, 0 and the link transmission rate (i.e., either packets from the flow are being transmitted on the link or not). The measurement of throughput can be tricky since we are interested in an average of the instantaneous transmission rate over some interval of time. A flow is said to be backlogged whenever the corresponding queue contains packets to be transmitted on link. The evaluation of the average transmission rate for a flow is usually taken over a period of time during which the flow is continuously backlogged and is given as the number of bits transmitted over an arbitrary interval during the busy period. Again, if this period is too small, then we could see large fluctuations in the transmission rate. Over longer periods of time, including several periods during which a flow is backlogged, the throughput for a ``stable'' flow will match the average arrival rate of the flow (the definition of stability). Otherwise, we are in a situation in which the queue for a particular flow can grow without bound and buffer overflow becomes the primary concern. To ensure stability and also to meaningfully discuss packet delay (the interval of time from which the packet enters the system until it is transmitted), one has to make assumptions regarding the nature of the packet sources such as their average and peak bandwidths. Often the assumptions regarding source characteristics are enforced (shaped) by an appropriate regulator such as the, so called, leaky bucket regulator which effectively constrains the average bandwidth and the ``burstiness'' of the traffic.
Fairness is a measure of how close the server comes to Generalized Processor Sharing (GPS) [9] when serving simultaneously backlogged flows. GPS is an idealized model in which the capacity of the link is assumed to be infinitely divisible and can be shared among an number of flows simultaneously as long as the capacity of the link is not exceeded. The primary purpose of the fairness criterion is to isolate the behavior of one flow from another.
With any QoS support, it is necessary to have a way of prescribing the
level of support that is required.
Much of the research in link scheduling assumes that the QoS
requirement for each flow is specified by a single number having
the interpretation of a (dimensionless) weight or a rate.
Suppose flow i has an associated weight given by a positive real
number  and C denotes the capacity of the output
link in bits per second (bps).
Then the usual interpretation of the
and C denotes the capacity of the output
link in bits per second (bps).
Then the usual interpretation of the  's is that, ideally,
whenever a flow i is backlogged it will transmit
packets at an average rate which is no less than
's is that, ideally,
whenever a flow i is backlogged it will transmit
packets at an average rate which is no less than
 (bps).
The determination of QoS parameters, such as delay, delay jitter,
throughput and fairness, does not directly follow from the weights
of backlogged flows but depends on the total weight of backlogged flows,
and on the specific algorithm used by the link scheduler.
This indirect way of specifying QoS requirements makes admission control difficult.
Also, using weights to guarantee delay bounds results in underutilization.
(bps).
The determination of QoS parameters, such as delay, delay jitter,
throughput and fairness, does not directly follow from the weights
of backlogged flows but depends on the total weight of backlogged flows,
and on the specific algorithm used by the link scheduler.
This indirect way of specifying QoS requirements makes admission control difficult.
Also, using weights to guarantee delay bounds results in underutilization.
The delay and delay jitter requirements can be somewhat decoupled from the throughput requirements by using regulators (shapers) which release packets to the link scheduler at the appropriate times. Such regulator-scheduler combinations can result in policies that may not transmit packets even when packets are available for transmission. Delay-earliest due date [3] provides delay bounds independent of the bandwidth guaranteed to a flow, however, at the cost of reserving bandwidth at the peak rate.
We next turn to QoS parameters in operating systems (OS). Unlike link scheduling, in the operating system context there are multiple resources, such as the CPU, disks, and network interfaces, that are shared among competing processes. Each of the servers (resources) is capable of delivering ``work'' at a certain rate. For example, a CPU executes instructions at 100 Million Instructions Per Second (MIPS), a disk can transfer a data block (512 bytes) in 12 milliseconds, and a network interface can deliver bits on its output link at 10 Million bits per second (Mbps).
Processes in the OS context roughly correspond to flows and are modeled as a sequence of phases where each phase consists of the name of a server and the corresponding amount of ``work.'' For example, (CPU, 100 million instructions) is a phase that specifies the CPU as the server and the work which consists of executing 100 million instructions. The amount of time taken by the phase depends on the rating of the CPU server-a 100 MIPS CPU will take 1 second to complete this phase. At the completion of a phase, the process will move to the next phase which consists of a new server and work requirement. In the actual system, the phases (server and work requirements) are not known in advance.
Since we model processes as a sequence of phases, any delay incurred while completing a phase will be propagated to all subsequent phases. Thus we think of a process as a ``closed-loop'' source. Conversely, if a process gains a time advantage by getting extra service, this advantage is also passed on to subsequent phases. One could also consider ``open-loop'' processes in which the time-of-arrival of a phase is independent of previous phases. For example, if the phases of a process were generated by interrupts, it is possible for a new phase to arrive before the previous phase completes its service. We do not consider ``open-loop'' processes in this paper.
In the link scheduling environment the scheduler transmits one packet-at-a-time over the link. We assume in the OS context that each server has a preemption interval which specifies the temporal boundaries where preemptions may occur. This means that the ``granularity'' of sharing is determined by the properties of the server and the scheduler.
In order to specify QoS requirements,
we associate with each process and
each server a reservation, called a service fraction,
which gives the amount of the server required by the process.
For example, suppose a process has a .25 reservation on the CPU.
In the case of a 100MIPS CPU, this means that the process needs
at least a 25MIPS CPU to meet its performance objectives.
The weights,  , defined in the section on link scheduling determine service
fractions as ratios
, defined in the section on link scheduling determine service
fractions as ratios  .
We choose to use service fractions since they reflect, in absolute terms, the
service requirement of the process and thereby simplify admission control.
.
We choose to use service fractions since they reflect, in absolute terms, the
service requirement of the process and thereby simplify admission control.
The performance objective most readily specified by reservations is a cumulative service guarantee, which means a guarantee that the real system will keep pace with an ideal execution based on the server reservations. For example, suppose a process reserves 20% of the CPU and 50% of the disk I/O subsystem and suppose the CPU is rated at 100 MIPS and the disk I/O subsystem can do single block (4 Kbytes) transfer in 12 milliseconds. According to the reservation, this process should ``see'' at least a 20 MIPS CPU and a disk I/O subsystem capable of transferring a single block in 24 milliseconds. Suppose the process alternates between CPU and disk I/O phases where each CPU phase requires the execution of 4 million instructions and each disk I/O phase consists of 6 random block transfers. Accordingly, the process should take no more than 200 ms for each CPU phase and 144 ms for each disk I/O phase regardless of the number of process phases and competing processes.
Other QoS parameters for processes can be defined. If we were to associate the phases of a process with the packets of a flow we obtain the following notion of delay. The delay of a phase at a particular server is the cumulative time spent by the phase either waiting for the server or running on the corresponding server. It is not difficult to see that guaranteeing delay bounds (i.e., bounding the time it takes to complete a phase) is not sufficient to provide a cumulative service guarantee. This is because the phase delays can accumulate (in the closed-loop case) over multiple phases leading to an unbounded discrepancy between the actual and the ideal cumulative service. For example, phase delays on one server may reduce the the service rate of other servers in a closed loop system.
We also define the notion of fairness which measures the ability of the system to ensure that processes simultaneously contending for the same server will ``share'' that server in proportion to their reservations. Fairness in the OS context, sometimes referred to as proportional sharing [11, 5, 10], is problematic since the cost of providing fairness (context switching) increases as the granularity of server sharing decreases. It is also not clear that fine-grain sharing is always desirable in a general-purpose operating system, particularly for ``batch'' processes where coarse-grain sharing is acceptable and substantially reduces the context switching overhead.
Recently proposed scheduling algorithms which are most closely related to our work are: Stride scheduling [11], which attempts to provide each process with a share of the server in proportion to its corresponding weight (number of ``tickets''); start-time fair queuing [5], which is based on the corresponding link scheduling algorithm [6]; and earliest eligible virtual deadline first [10], which provides each process with a share of the server in proportion to its corresponding weight; and the CPU scheduling policy presented in [8], which provides each process with its reserved share. These algorithms were not designed with our cumulative service measure in mind, so it is not surprising that the properties they do enjoy are not sufficient to provide a cumulative service guarantee.
In the next section we introduce our system and process models and give formal definitions of the terms used in the remainder of this paper.
A system consists of a
collection,  , of servers (e.g., CPU, disk,
and network).
Each server
, of servers (e.g., CPU, disk,
and network).
Each server  is characterized by a service rate
is characterized by a service rate
 and a preemption interval,
and a preemption interval,  .
If
.
If  is an amount of work to be accomplished by server s, then the time
to complete
is an amount of work to be accomplished by server s, then the time
to complete  on server s is
on server s is
 .
When a ``process'' is run on a server with a positive preemption interval
.
When a ``process'' is run on a server with a positive preemption interval
 ,
the running time must be an integral multiple of
,
the running time must be an integral multiple of  and
the process can only be preempted at integral multiples of
and
the process can only be preempted at integral multiples of  .
The limiting case of
.
The limiting case of  corresponds
to a server for which running times are arbitrary and preemptions
are not restricted.
corresponds
to a server for which running times are arbitrary and preemptions
are not restricted.
A phase
is a server-duration pair, (s, t), where  and
t is the amount of time it would take server s to complete
the phase running alone on the server.
An equivalent definition of a phase (s,t) is a server-work pair,
and
t is the amount of time it would take server s to complete
the phase running alone on the server.
An equivalent definition of a phase (s,t) is a server-work pair,  ,
where
,
where  .
.
A process
is a sequence
(finite or infinite) of phases,
 .
The phases of a process are not known in advance.
Initially, the only thing we know about a process is the identity of the
first server, i.e.,
.
The phases of a process are not known in advance.
Initially, the only thing we know about a process is the identity of the
first server, i.e.,  .
By running P on server
.
By running P on server  we will eventually learn
we will eventually learn  ,
the duration of the first phase, and
,
the duration of the first phase, and  ,
the server required for the second phase,
i.e.,
,
the server required for the second phase,
i.e.,  .
By running P on server
.
By running P on server  we eventually discover
we eventually discover  and the server required for the third phase,
viz.,
and the server required for the third phase,
viz.,  , and so on.
, and so on.
Let  denote the sequence of times that
processes
denote the sequence of times that
processes  enter the system.
The departure time of a process depends upon the process and the
scheduling discipline.
We assume that
each process has a (possibly infinite) departure time.
A process
enter the system.
The departure time of a process depends upon the process and the
scheduling discipline.
We assume that
each process has a (possibly infinite) departure time.
A process  is active at time t if
is active at time t if
 and the departure time of process
and the departure time of process  is greater
that t.
Let
is greater
that t.
Let  denote the set of indices of active processes at
time t.
denote the set of indices of active processes at
time t.
We assume that each process  ,
before being admitted to the system, specifies a
service fraction for each server s, namely,
,
before being admitted to the system, specifies a
service fraction for each server s, namely,  .
We require for all
.
We require for all  that
that
 .
That is,
the sum of the service fractions of all active processes with respect to server
s does not exceed 1.
.
That is,
the sum of the service fractions of all active processes with respect to server
s does not exceed 1.
Even though we are interested in the performance of our system over
all servers it is sufficient to study the performance at a single
server.
From the point of view of server s,
a process is denoted by a sequence of phases that alternate
between server s and elsewhere, i.e.,
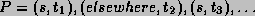 or
or
 .
The ``elsewhere'' server represents the phases of processes at
servers other than s.
.
The ``elsewhere'' server represents the phases of processes at
servers other than s.
A process arrives at server s if it enters the system at server s or it requires server s after completing a phase at the elsewhere server. The process arrival times at server s depend upon the duration of the phases and the scheduling policies used at the various servers. A process leaves server s whenever it completes a phase at server s. When a process leaves server s it will either eventually depart the system or arrive at server s for another phase.
Since we are considering the performance at a single server,
say s, we can drop references to server s since it is understood.
Therefore B denotes the service rate of the server,
 denotes
the preemption interval of the server,
and
denotes
the preemption interval of the server,
and  denotes the service fraction of process
denotes the service fraction of process  .
.
When a process is run on a server it is assigned a maximum running
time which we call a quantum.
The scheduling algorithm is not required to use a fixed size quantum.
Scheduling decisions are made at points in time called
decision epochs which correspond to the expiration of the
current quantum, the completion of the phase of the current running
process, or the end of the current preemption interval
following the arrival of a process at the server.
In the latter case, if the arrival of a process occurs at time
 while the server is in the midst of a preemption interval,
while the server is in the midst of a preemption interval,
 , then the scheduler must wait until
, then the scheduler must wait until  ,
that is, the decision epoch occurs at
,
that is, the decision epoch occurs at  .
At each decision epoch,
the current process can be preempted
and the
the scheduler can assign a new process
to the server.
.
At each decision epoch,
the current process can be preempted
and the
the scheduler can assign a new process
to the server.
Realizable scheduling policies require that we run at most one process at a time
on the server.
This means that if there is more than one process waiting to run on
the server, then one or both of the processes will
experience (queuing) delay.
Although we do not show the dependency of the following quantities on the
scheduling policy, it is important to keep this dependency in mind.
Let  be an arbitrary real time interval.
We define
be an arbitrary real time interval.
We define  and
and  to be the
cumulative real waiting time (blocked by other processes running on the server)
and real service time (running on the server), respectively, obtained
by process
to be the
cumulative real waiting time (blocked by other processes running on the server)
and real service time (running on the server), respectively, obtained
by process  in the interval
in the interval  .
For
.
For  we define
we define  and
and  .
.
Let  and
for
and
for  define
define  .
By definition,
.
By definition,  is the total time spent
by process
is the total time spent
by process  at the server in the interval
at the server in the interval 
The quantities just defined are illustrated in Figure 1. The heavy line denotes the accumulation of waiting time and service time of a process at the server. The slope of this curve is either 1 or 0 depending on whether the process is at the server or elsewhere, respectively. From the figure we see that the process arrives at the server at time 4 and leaves at time 17 for elsewhere. The process arrives again at time 23. The lower lighter curve, labeled with 1, represents the service obtained by the process (an explanation for the curve labeled with 1/2 is coming). This curve has slope 1 or 0 depending on whether the process is being served or waiting, respectively. Since the process leaves at time 17, it means that the service requirement of the phase is 6. Intervals on the time axis are labeled with e, w, or s, depending on whether the process is elsewhere, waiting, or being served, respectively. We can read off the following quantities from the figure: r(4,17) = 13; w(4,17) = 7; s(4,17) = 6; r(12,23) = 5; w(12, 23) = 2; s(12, 23) = 3.
To evaluate the performance of our scheduling algorithm, we introduce a processor sharing model in which the server can run any number of processes simultaneously as long as the sum of their service fractions does not exceed one. In the processor sharing model, processes do not block one another since they can run simultaneously on the server, albeit at a reduced rate. We refer to the service time in the processor sharing model as virtual service time.
A process with service fraction  that receives t units of
real service time
would take
that receives t units of
real service time
would take  virtual service time units to obtain the same amount of
service under processor sharing running at rate
virtual service time units to obtain the same amount of
service under processor sharing running at rate  .
Conversely,
a phase taking v units of virtual service time to complete under the processor
sharing model requires
.
Conversely,
a phase taking v units of virtual service time to complete under the processor
sharing model requires
 real service time on the real server.
real service time on the real server.
Let  denote the cumulative virtual service time obtained by
process
denote the cumulative virtual service time obtained by
process  in the interval
in the interval  .
For
.
For  we define
we define  .
Note that
.
Note that 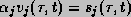 and
and
 for
for  .
.

Figure 1:
Example of Cumulative Service.
In Figure 1 the curve label 1/2 denotes the virtual service time accrued by a process with a service fraction equal to 1/2. Accordingly, the slope of this curve is either 2 or 0 depending on whether the process is being served or not, respectively. Therefore the phase of duration 6 (from time 4 to 17) requires 12 units of virtual service time to complete.
Definition 1: We say that a scheduling policy provides
a cumulative service guarantee
if there exists a constant K such that for all processes  and
and  , we have
, we have
 .
.
From Figure 1 we have:
v(4,9) = 0; r(4,9) = 5, and
v(9,14)= 6; r(9,14) = 5, and
v(4,23)= 12; r(4,23) = 13.
Considering the portion of the process illustrated in Figure 1,
we conclude that  for all
for all  and
and  .
.
Another interpretation of the cumulative service guarantee is that the total real time taken to provide a process with service (including the waiting time and the service time) is no more than a constant amount of time more than the virtual service time required for an equivalent amount of real service.
Although the definition of cumulative service guarantee is in terms of a single server, it implies a ``global'' cumulative service guarantee (using cumulative virtual service time and cumulative real time over all servers) in the multi-server case where there is a constant number of servers.
Example 2: Consider a process P=
 ,
,  ,
,  ,
,  ,
,
 .
that requires servers
.
that requires servers  and
and  ,
and reserves
,
and reserves  and
and  fractions of
fractions of
 and
and  , respectively.
Also, let
, respectively.
Also, let  and
and  be the
cumulative service bound on servers
be the
cumulative service bound on servers  and
and 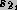 respectively.
In a system that guarantees cumulative service,
the total real time for the servers to provide
[ _i=1^n2 t_2i-1 +
_i=1^n2 t_2i
]
time units of service (waiting plus service time)
is bounded by
[ 1 _i=1^n2 t_2i-1 +
1 _i=1^n2 t_2i + K_1 + K_2 .
]
This is in contrast to other scheduling policies
(e.g., [8, 11, 5, 10])
that provide delay bounds on a per phase basis.
In this case the discrepancy between the cumulative service obtained and the
time to acquire this service can grow with n, the number of phases.
respectively.
In a system that guarantees cumulative service,
the total real time for the servers to provide
[ _i=1^n2 t_2i-1 +
_i=1^n2 t_2i
]
time units of service (waiting plus service time)
is bounded by
[ 1 _i=1^n2 t_2i-1 +
1 _i=1^n2 t_2i + K_1 + K_2 .
]
This is in contrast to other scheduling policies
(e.g., [8, 11, 5, 10])
that provide delay bounds on a per phase basis.
In this case the discrepancy between the cumulative service obtained and the
time to acquire this service can grow with n, the number of phases.

Definition 2: We say that a scheduling policy provides
delay bound if, for any process 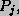 the real waiting time plus service time to complete a phase of
duration d takes at most
a constant amount more than
the real waiting time plus service time to complete a phase of
duration d takes at most
a constant amount more than  .
.

A ``fair'' scheduling policy ensures that multiple processes requiring the same server share the server in proportion to their reservations, independent of their previous usage of the resource [2]. That is, a fair scheduling policy does not penalize a process that utilized an idle server beyond its reservation when other processes become active on that server.
Definition 3: A scheduling policy is
fair
if there exists a constant D such that
for any time interval  during which
a pair of processes,
during which
a pair of processes,  and
and  , both continuously require the server,
we have
, both continuously require the server,
we have
 .
.

Processor sharing provides ideal fairness [9]. However, processor sharing cannot be implemented and thus a host of scheduling policies that aim to provide bounded fairness and/or delay properties have been devised for link scheduling [2, 13, 4, 5]. As we mentioned earlier, the cost of providing fine-grain fairness (proportional sharing [11, 5, 10]) is high and not always justified in the OS context. However, fairness is important when services are overloaded and it is necessary for all impacted processes to make steady, and proportional, progress.
In this section we present a new scheduling policy, called Move-To-Rear List Scheduling, which provides a cumulative service guarantee, is fair, and has bounded delay. In the following subsection we present the MTR-LS policy followed by a subsection which contains formal statements and proofs of the properties of the MRT-LS policy.
Central to the MTR-LS policy is an ordered list,  ,
of the processes that are active at any time.
We say a process on the list
,
of the processes that are active at any time.
We say a process on the list  is runnable
if it is not elsewhere.
The MTR-LS policy services the runnable processes in the order that
they appear on the list
is runnable
if it is not elsewhere.
The MTR-LS policy services the runnable processes in the order that
they appear on the list  .
.
The MTR-LS policy makes use of a constant T, which we call the
virtual time quantum.
Associated with each process  on the list
on the list  is a value
is a value
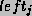 .
The initial value of
.
The initial value of 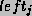 is
is
 .
When processes are serviced, they run for a quantum which is bounded by
the value in
.
When processes are serviced, they run for a quantum which is bounded by
the value in 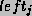 .
At the end of the service period,
.
At the end of the service period, 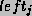 is decremented by the actual amount
of service time that the process obtained
and if the result is zero, then
is decremented by the actual amount
of service time that the process obtained
and if the result is zero, then  is moved to the rear
of the list
is moved to the rear
of the list  and the value of
and the value of 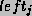 is reset to
is reset to  .
The value
.
The value  is the real time quantum.
A process that advances by
is the real time quantum.
A process that advances by  real service time,
advances by T virtual service time.
real service time,
advances by T virtual service time.
The service obtained by a process can be less than the allocated
quantum due to the termination of a phase or the arrival of a process.
In the former case, the phase terminates, the process goes elsewhere, and
the first runnable process on  is serviced next.
In the latter case, if the arriving process is ahead of the
current running process
in the list
is serviced next.
In the latter case, if the arriving process is ahead of the
current running process
in the list  , then the running process is preempted (as soon
as the preemption interval permits) and the
first runnable process on
, then the running process is preempted (as soon
as the preemption interval permits) and the
first runnable process on  is serviced next.
is serviced next.
The description of the MTR-LS policy depends on a few mechanisms which we
give next.
Whenever a new process,  , enters the system it is added to the
end of
, enters the system it is added to the
end of  and
and 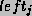 is set equal to
is set equal to
 where T is a system constant.
As long as the process is in the system, whether it is at the
server or elsewhere, it appears in the list
where T is a system constant.
As long as the process is in the system, whether it is at the
server or elsewhere, it appears in the list  .
Whenever a process departs the system it is removed from
.
Whenever a process departs the system it is removed from  .
.
Whenever all the processes in  are elsewhere the server is idle.
Otherwise the server is running a process and the state is busy.
Decision epochs correspond to the expiration of the
current quantum, the completion of the phase of the current running
process, or the end of the current preemption interval
following the arrival of a process at the server.
In the latter case, if the arrival of a process occurs at time
are elsewhere the server is idle.
Otherwise the server is running a process and the state is busy.
Decision epochs correspond to the expiration of the
current quantum, the completion of the phase of the current running
process, or the end of the current preemption interval
following the arrival of a process at the server.
In the latter case, if the arrival of a process occurs at time
 while the server is in the midst of a preemption interval,
while the server is in the midst of a preemption interval,
 , then the scheduler must wait until
, then the scheduler must wait until  ,
that is, the decision epoch occurs at
,
that is, the decision epoch occurs at  .
.
The command wait causes the scheduler to ``sleep'' until the next decision epoch. Whenever a process starts running, a timer, called elapsed, is started from zero. elapsed can be used to determine the service obtained by the currently running process.
Run_a_Process if there is no runnable process on the listFigure 2: Routine Run_a_Process.then state = idle; else Let
be the first runnable process on the list
; state = busy; run
on the server for at most
time units (current quantum) and start elapsed timer; wait;
The routine Run_a_Process, shown in Figure 2, is called to
select the next process to run on the server.
Run_a_Process looks for the first runnable process on the
list  .
If the list
.
If the list  does not contain a runnable process then the server
state is set to idle and the scheduler waits for the next
decision epoch.
Otherwise the first runnable process on
does not contain a runnable process then the server
state is set to idle and the scheduler waits for the next
decision epoch.
Otherwise the first runnable process on  is selected and run for
a quantum of at most
is selected and run for
a quantum of at most 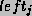 time units.
The server state is set to busy and the scheduler waits for the next
decision epoch.
The variable elapsed will record the elapsed time to the next
decision epoch.
time units.
The server state is set to busy and the scheduler waits for the next
decision epoch.
The variable elapsed will record the elapsed time to the next
decision epoch.
The Move-To-Rear List Scheduling policy is shown in Figure 3.
The MTR-LS policy is called at each decision epoch.
It determines if a process was running in the interval
leading up to this decision epoch by
checking to see if the state is busy.
If so, it decrements the corresponding 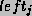 by
the elapsed time since the previous decision epoch.
If the resulting value of
by
the elapsed time since the previous decision epoch.
If the resulting value of 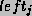 is zero
the corresponding process is moved
to the end of the list
is zero
the corresponding process is moved
to the end of the list  and
and
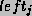 is reset to
is reset to  .
.
Under the MTR-LS policy there are two
ways for a runnable process to be blocked.
First, it can be blocked by runnable processes
ahead of it on the list  .
Second, for servers with a positive preemption interval (
.
Second, for servers with a positive preemption interval (  ),
a runnable process can be blocked by processes that are behind
it on the list
),
a runnable process can be blocked by processes that are behind
it on the list  .
This happens when a process arrives at the server while another
process is running and in the midst of a preemption interval.
If the arriving process is ahead of the running process in the list
.
This happens when a process arrives at the server while another
process is running and in the midst of a preemption interval.
If the arriving process is ahead of the running process in the list
 , then the arriving process will be blocked at least
until the end of the current preemption interval.
This kind of blocking is called
, then the arriving process will be blocked at least
until the end of the current preemption interval.
This kind of blocking is called  -blocking.
It is important to notice that if a process is
-blocking.
It is important to notice that if a process is  -blocked then,
because of its position in the list
-blocked then,
because of its position in the list  ,
it will obtain service before the process that caused the
,
it will obtain service before the process that caused the  -blocking
returns to service.
-blocking
returns to service.
Initialization
For each process  , which is active at time 0,
put
, which is active at time 0,
put  on the list
on the list  (in any order)
and set
(in any order)
and set 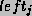 =
= 
Run_a_Process;
The Method
(Runs at each decision epoch)
Decision epochs correspond to the expiration of the
current quantum, the completion of the phase of the current running
process, or the end of the current preemption interval
following the arrival of a process at the server
if state == busy then
Let  be the current running process;
be the current running process;
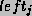 =
= 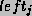 - elapsed;
if
- elapsed;
if 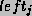 == 0 then
Move
== 0 then
Move  to the rear of the list
to the rear of the list  ;
;
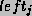 =
=  ;
Run_a_Process;
;
Run_a_Process;
A straight-forward implementation of MTR-LS stores the runnable processes in  in a heap [1].
When a process is moved to the rear of
in a heap [1].
When a process is moved to the rear of  it is given a new largest timestamp.
Arriving processes and runnable processes that are moved to the
rear of the list are inserted into the heap in O( ln(n) ) time
where n is the number of runnable processes in
it is given a new largest timestamp.
Arriving processes and runnable processes that are moved to the
rear of the list are inserted into the heap in O( ln(n) ) time
where n is the number of runnable processes in  .
The runnable process with the smallest timestamp (corresponds to the
first runnable process in the list
.
The runnable process with the smallest timestamp (corresponds to the
first runnable process in the list  ) can be found in
constant time.
It takes O(ln(n)) time to rebuild the heap when the first process
is removed from the heap and is no longer runnable (i.e., gone elsewhere).
) can be found in
constant time.
It takes O(ln(n)) time to rebuild the heap when the first process
is removed from the heap and is no longer runnable (i.e., gone elsewhere).
Lemma 1: The complexity of MTR-LS is O(ln(n))
where n is the number of
active processes.

The MTR-LS policy provides a fairness guarantee whose ``granularity'' depends on T, the virtual quantum. Unlike other QoS parameters, the fairness guarantee does not depend on the length of the preemption interval or whether the sum of the service fractions is less than or equal to one.
Lemma 2: The MTR-LS policy is fair with a bound of 2 T.
That is, for any real time interval  during which
during which  and
and  are
both continuously runnable
[
|s_i(, t)/ _i - s_j(, t) / _j| 2T .
]
are
both continuously runnable
[
|s_i(, t)/ _i - s_j(, t) / _j| 2T .
]
Proof:
The worst case situation occurs when one of the processes, say  , is ahead
of
, is ahead
of  on the list and
on the list and 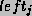 is extremely small (
is extremely small (  ).
It is possible for
).
It is possible for  to gain T units of virtual time, then
for
to gain T units of virtual time, then
for  to run for
to run for  units of virtual time
and be placed at the back of the list.
If
units of virtual time
and be placed at the back of the list.
If  were to run for another T units of virtual time, then
the accrued virtual time of
were to run for another T units of virtual time, then
the accrued virtual time of
 would be ahead of the accrued virtual time
of
would be ahead of the accrued virtual time
of  by a value which is bounded by 2T.
by a value which is bounded by 2T.

It is easy to see from the proof that the MTR-LS policy supports
proportional sharing for processes with arbitrary, non-negative service
fractions.
However, the cumulative service and delay guarantees are dependent upon
the service fractions and the length of the
preemption interval.
In the next subsection we treat the case of a zero-length preemption interval
followed by a subsection on the case  .
.
 Case
Case
Throughout we assume that we are using the MTR-LS policy.
Assuming  ,
,  denotes the value of the variable
denotes the value of the variable 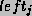 at real time t.
at real time t.
The following is the basic lemma for the case  .
.
Lemma 3:
Assume  and
and  . Then
for all
. Then
for all  we have
we have
Proof:
The idea of the proof is to construct a scenario,  ,
whereby process
,
whereby process  obtains service only after being blocked
to the maximum extent possible by the other processes.
It will follow from the construction that for
any other execution in which
obtains service only after being blocked
to the maximum extent possible by the other processes.
It will follow from the construction that for
any other execution in which  obtains the
same amount of service, the amount of blocking by other
processes will be no greater that
obtains the
same amount of service, the amount of blocking by other
processes will be no greater that  .
We show that in this extremal case that the lemma holds and therefore it
holds for all other executions.
The notation
.
We show that in this extremal case that the lemma holds and therefore it
holds for all other executions.
The notation  means that
the second argument has some appropriate value.
We use this notation to avoid having to create new symbols for these
values.
means that
the second argument has some appropriate value.
We use this notation to avoid having to create new symbols for these
values.
The execution  is designed to insure that
is designed to insure that  is blocked from
running to the maximum extent possible.
With this in mind, we assume
that at time
is blocked from
running to the maximum extent possible.
With this in mind, we assume
that at time  all processes
all processes  with
with  and
and  are ahead of
are ahead of  in the list
in the list  .
Also assume that all of these processes run to their maximum
extent,
.
Also assume that all of these processes run to their maximum
extent,  while preventing
while preventing  from running.
Thus
from running.
Thus  , the real time spent by process
, the real time spent by process  waiting to run,
without running,
is bounded by
waiting to run,
without running,
is bounded by  .
At this point we have:
[
r_j(,) (1-_j) T + v_j(,)
]
From this point on
.
At this point we have:
[
r_j(,) (1-_j) T + v_j(,)
]
From this point on  cannot be blocked further until
cannot be blocked further until
 obtains
obtains  real service time.
At the point where
real service time.
At the point where  obtains
obtains  service time we have:
[
r_j(,) (1-_j)(T - left_j()/_j) + v_j(,)
]
Now
service time we have:
[
r_j(,) (1-_j)(T - left_j()/_j) + v_j(,)
]
Now  is at the back of the list and so the worst case is for all the
active processes to run to their maximum extent
while blocking
is at the back of the list and so the worst case is for all the
active processes to run to their maximum extent
while blocking  from running.
At the point when
from running.
At the point when  reaches the head of the list
and can no longer be blocked we have:
[
r_j(,) (1-_j)(2 T - left_j()/_j) + v_j(,)
]
reaches the head of the list
and can no longer be blocked we have:
[
r_j(,) (1-_j)(2 T - left_j()/_j) + v_j(,)
]
Continuing as above, after every time  advances by T the
other processes can only block
advances by T the
other processes can only block  by at most
by at most  .
Since the real running time is
.
Since the real running time is  , the
virtual time advance equals the worst-case real-time blocking
and service times.
Thus the above inequality is the worst case for the execution
, the
virtual time advance equals the worst-case real-time blocking
and service times.
Thus the above inequality is the worst case for the execution  .
.
Finally, it is easy to observe that for any other execution
the amount of blocking by other processes for the same amount
of running time for  is no larger than the
scenario
is no larger than the
scenario  given above.
The lemma follows.
given above.
The lemma follows.

Corollary 1:
The MTR-LS policy provides a cumulative service guarantee.

From Lemma 3 we can write  for all
j and
for all
j and  .
We obtain this worst-case bound by setting
.
We obtain this worst-case bound by setting 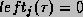 and
and  .
For the case where
.
For the case where  we get
we get
 since
since  .
.
Corollary 2: The MTR-LS policy provides bounded delay.
Proof:
Consider a phase of process  that requires
that requires  work.
The duration of the phase is
work.
The duration of the phase is  and the allotted virtual time
is equal to
and the allotted virtual time
is equal to  .
Let
.
Let  be the beginning of the phase and t the time
the phase ends under the MTR-LS policy.
Using Equation 1 we get
[
r_j(,t) /(_j B) + (1-_j)(2 T - left_j()/_j) .
]
This equation states that the amount of real time taken to complete
this phase is at most a constant amount of time
more than
be the beginning of the phase and t the time
the phase ends under the MTR-LS policy.
Using Equation 1 we get
[
r_j(,t) /(_j B) + (1-_j)(2 T - left_j()/_j) .
]
This equation states that the amount of real time taken to complete
this phase is at most a constant amount of time
more than  times the duration of the phase.
times the duration of the phase.

 Case
Case
Assume that the server has a positive preemption
interval ( i.e.,  ).
As we described above, when the preemption interval is positive, we
have to deal with the case
in which a process
).
As we described above, when the preemption interval is positive, we
have to deal with the case
in which a process  arrives at the server while the server
is running process
arrives at the server while the server
is running process  and is in the midst of a preemption interval.
In this case the next decision epoch occurs at the
end of the current preemption interval.
and is in the midst of a preemption interval.
In this case the next decision epoch occurs at the
end of the current preemption interval.
For example, let's consider a system in
which there are two processes  and
and  .
In this system, process
.
In this system, process  runs continuously on the server and process
runs continuously on the server and process
 alternates between the server and the elsewhere server.
We also assume that whenever process
alternates between the server and the elsewhere server.
We also assume that whenever process  runs on the server it runs for
exactly one preemption interval and then goes to elsewhere for
a while.
Due to incredible bad luck,
whenever process
runs on the server it runs for
exactly one preemption interval and then goes to elsewhere for
a while.
Due to incredible bad luck,
whenever process  arrives at the server, the server is
running process
arrives at the server, the server is
running process  and is exactly
at the beginning of the current preemption interval.
Therefore
process
and is exactly
at the beginning of the current preemption interval.
Therefore
process  has to wait (this is
has to wait (this is  -blocking)
-blocking)
 real time units before running on
the server.
This sequence of
real time units before running on
the server.
This sequence of  -blocking can persist for
-blocking can persist for  time units before
time units before
 is put to the rear of
is put to the rear of  .
In addition to the bad luck with
.
In addition to the bad luck with  -blocking,
whenever
-blocking,
whenever  is put at the end of the list
is put at the end of the list  , process
, process  blocks
blocks  for
for  time units.
Thus we find that,
time units.
Thus we find that,  , the real time
spent at the server in pursuit of T units of virtual time service,
can be as large as
, the real time
spent at the server in pursuit of T units of virtual time service,
can be as large as
 .
From this it appears that
.
From this it appears that  is sufficient
to have a cumulative service guarantee for process
is sufficient
to have a cumulative service guarantee for process  on the server.
Interchanging the roles of
on the server.
Interchanging the roles of  and
and  ,
we get that
,
we get that  is sufficient
to have a cumulative service guarantee for process
is sufficient
to have a cumulative service guarantee for process  on the server.
on the server.
As this example shows, in order to have a cumulative service guarantee we need additional restrictions on the service fractions associated with servers having a positive preemption intervals. The following result gives a sufficient condition on the service fractions associated with the server such that the MTR-LS policy supports a cumulative service guarantee.
Lemma 4:
Assume  .
Assume that for all t and all
.
Assume that for all t and all  we have
we have
 .
Then for all
.
Then for all  we have
we have
Proof:
The proof on this lemma is similar to the proof of Lemma 3.
We construct a scenario,  ,
whereby process
,
whereby process  obtains service only after being blocked
to the maximum extent possible by the other processes.
In addition to the blocking used in the proof
of Lemma 3, this construction uses
obtains service only after being blocked
to the maximum extent possible by the other processes.
In addition to the blocking used in the proof
of Lemma 3, this construction uses  -blocking
(See Step 2 of the MTR-LS policy) to increase the amount of
blocking that process
-blocking
(See Step 2 of the MTR-LS policy) to increase the amount of
blocking that process  incurs.
It follows from the construction that for
any other execution in which
incurs.
It follows from the construction that for
any other execution in which  obtains the
same amount of service, the amount of blocking by other
processes will be no greater than
obtains the
same amount of service, the amount of blocking by other
processes will be no greater than  .
We show that in this extremal case that the lemma holds and therefore it
holds for all other executions.
.
We show that in this extremal case that the lemma holds and therefore it
holds for all other executions.
The execution  is designed to insure that
is designed to insure that  is blocked from
running to the maximum extent possible.
Assume that at time
is blocked from
running to the maximum extent possible.
Assume that at time  all processes
all processes  with
with  and
and  are ahead of
are ahead of  in the list
in the list  .
Also assume that all of these processes run to their maximum
extent,
.
Also assume that all of these processes run to their maximum
extent,  while preventing
while preventing  from running.
Thus
from running.
Thus  , the real time spent by process
, the real time spent by process  waiting to run,
without running,
is bounded by
waiting to run,
without running,
is bounded by  .
At this point we have:
[
r_j(,) (1-_j) T + v_j(,)
]
In the proof of Lemma 4.2.1 process
.
At this point we have:
[
r_j(,) (1-_j) T + v_j(,)
]
In the proof of Lemma 4.2.1 process  could no longer
be blocked until is obtained
could no longer
be blocked until is obtained  real service time.
However, due to the positive preemption interval of the server, process
real service time.
However, due to the positive preemption interval of the server, process
 can suffer
can suffer  -blocking while attaining
-blocking while attaining  service time.
Since process
service time.
Since process  has been blocked up to this point it has to run
a minimum of
has been blocked up to this point it has to run
a minimum of  before it goes to the elsewhere server.
When process
before it goes to the elsewhere server.
When process  arrives from the elsewhere server we assume that
some other process is in service and that
arrives from the elsewhere server we assume that
some other process is in service and that  is
is  -blocked
for at most
-blocked
for at most  time units.
Then
time units.
Then  runs for
runs for  real time units and again goes to the
elsewhere server.
This pattern repeats until
real time units and again goes to the
elsewhere server.
This pattern repeats until  acquires
acquires  units of
processing time at which time we have:
[
r_j(,) (1-_j) T +
(2 _j - 1)left_j()/_j + v_j(,) .
]
Once again all the other processes are ahead of
units of
processing time at which time we have:
[
r_j(,) (1-_j) T +
(2 _j - 1)left_j()/_j + v_j(,) .
]
Once again all the other processes are ahead of  on the list
and can block
on the list
and can block  up to
up to  time units.
The result is that
time units.
The result is that  is once more at the head of the list
and we have:
[
r_j(,) (1-_j)2 T +
(2 _j - 1)left_j()/_j + v_j(,) .
]
From this point onward,
is once more at the head of the list
and we have:
[
r_j(,) (1-_j)2 T +
(2 _j - 1)left_j()/_j + v_j(,) .
]
From this point onward,  is
is  -blocked
every time it gains T units of virtual time and then
blocked by all the processes until it is reaches the head of the list.
Every iteration results in a gain of T virtual time for process
-blocked
every time it gains T units of virtual time and then
blocked by all the processes until it is reaches the head of the list.
Every iteration results in a gain of T virtual time for process
 during which it acquires
[
_j T - t + T _i A() _i
]
real time (
during which it acquires
[
_j T - t + T _i A() _i
]
real time (  -blocking,
ordinary blocking, and service time).
By assumption, the above quantity is less than T and
the lemma follows.
-blocking,
ordinary blocking, and service time).
By assumption, the above quantity is less than T and
the lemma follows.

Corollary 3:
Assume  .
Assume that for all t and all
.
Assume that for all t and all  we have
we have
 .
Then the MTR-LS policy provides a cumulative service guarantee.
.
Then the MTR-LS policy provides a cumulative service guarantee.

By setting  and
and  we get
we get
 for all j and
for all j and  .
In the case
.
In the case  , we have
, we have

Corollary 4:
Assume  .
Assume that for all t and all
.
Assume that for all t and all  we have
we have
 .
The MTR-LS policy provides bounded delay.
.
The MTR-LS policy provides bounded delay.

The major contributions of this paper are as follows: We introduced a new QoS parameter--cumulative service--for operating system scheduling to provide predictable performance for applications requiring multiple resources. The system we treat is dynamic, namely, processes enter and depart the system. Existing scheduling policies [8, 11, 5, 10] that provide delay or fairness do not guarantee cumulative service.
We have presented a new scheduling algorithm, called Move-To-Rear List Scheduling, which provides a cumulative service guarantee. Our results show that the MTR-LS policy provides a fairness bound of 2 T, where T is the virtual quantum of the server, regardless of the choice of service fractions. In a recent paper by Lund, Phillips, and Reingold [7], they mention an output link scheduling policy for ATM cells called ``Ideal Round Robin'' which is related to MTR-LS.
They do not analyze the properties of ``Ideal Round Robin'', but instead they use an approximation to ``Ideal Round Robin,'' called Fair Prioritized Round Robin, as a benchmark for comparison with a fair scheduling policy for an input-buffered switch [7].
The provision of other QoS parameters requires certain restrictions on the service
fractions.
These requirements provide the constraints for admission
control.
When arbitrary preemption is allowed (  ),
we require that the sum of the service fractions is less than or equal to one.
When preemption is allowed only at a multiple of the preemption interval
(
),
we require that the sum of the service fractions is less than or equal to one.
When preemption is allowed only at a multiple of the preemption interval
(  ),
we require that for all j,
),
we require that for all j,
 ,
where
,
where  is the set of active processes at time t.
This condition is easy to check since one need only check the
inequality for the largest service fraction.
As long as the above conditions on the service fractions
hold, the MTR-LS policy meets the cumulative service guarantee within
2 T and the delay bound is 2 T in the worst case. The
implementation complexity of MTR-LS is O(ln(n)) where n is the
number of processes.
is the set of active processes at time t.
This condition is easy to check since one need only check the
inequality for the largest service fraction.
As long as the above conditions on the service fractions
hold, the MTR-LS policy meets the cumulative service guarantee within
2 T and the delay bound is 2 T in the worst case. The
implementation complexity of MTR-LS is O(ln(n)) where n is the
number of processes.